2003/02/07(4)
[Algorithm & Data Structure] Heap Sort
アルゴリズムとデータ構造の試験前質問集 - No.3です
ソートは時間の関係上, もしかしたら他のを優先させるかもしれないし2回で終わるかもしれない, できるだけ原稿は落とさないつもり何回かに分けて書いていきます, 今回はHeapのみ扱ってみます
取り敢えずソートの回では単純なBubble Sortとか演習でやった挿入Sort, Quick Sortは解説の対象外にします
ソートされていない領域から最小のものを持ってきては一番上とSwapするだけ…選択ソートも単純なので此処では割愛させていただきますね
~教科書捜索中~
久しぶりにこのコーナーが始まりました, では早速始めましょう
教科書のp. 239, Heap Sortから順に解説します
取り敢えず今回やるソートとその特徴をまとめておきます
- (クイックソートQuick Sort O(n log n), 一般の条件では多分最速, 最悪の場合はO(n2))
- ヒープソートHeap Sort O(n log n), 半順序付き待ち行列, pp. 119-127, 実際にはp. 125が分かればOKPriority Queueの応用, 常に一定の速度で終わる
- ビンソートBin Sort O(n), 既に順序が確定している離散的なものの並び替えに利用できる
- 基数ソートRadix Sort O(n), Bin Sortの一般形, 例えば浮動小数点数とかはダメ離散的な型であれば有効なSort方法
- 併合ソートMerge Sort O(n log n), 他のソートが一般的にnデータを走査する回数パス x O(log n)に対してこれはこの辺は講義では触れていなかったけどね…log nパス x O(n)なのでディスク上のソート等に向いている
まずはHeap Sortから
上にも書いたとおり, これはHeapで表現された半獣所付き待ち行列の処理を応用してやるソート方法です
同じO(n log n)のQuick Sortに比べるとn og nの項につく定数係数の差遅いですが, Quick Sortは大抵の場合, 既にソートされている配列のソーティングにはかなり弱い(最悪の場合, O(n2))どんな最悪の場合でもO(n log n)の時間で計算できる利点があります
実際にソートの様子を書いてみると次のようになります
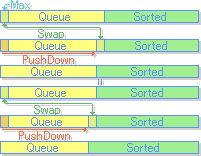
Priority QueueのHeapの先頭にある最小(or 最大)の要素を取り出し, swapによって要素を上に詰めるDeletemin(max)操作で最大要素をQueueと既にソートされた配列の境界にまで持って行き, そこまでを新たな"Sorted"領域とすることを要素数だけ繰り返せばソートが終わるという仕掛けです
このソートにかかる時間はPriority QueueをHeap上に作る(O(n))こととそれを使って全要素に対してDeleteソートする順序の逆順を返すPriority Queueである必要があるmax = Swap + PushDownを繰り返してHeapから追い出すこと(O(n log n))に大別されます
PushDownという処理を考えてみましょう, これは一部, 正確には先頭の要素だけが規則から外れたPriority Queueをswapによって正しいPriority Queueに変換する操作です, これは教科書のp.241 fig. 8.17を少し見れば明らかなようにO(log n)です
これはPriority QueueのDeletemax操作のうち, 半順序の回復の操作に当たる部分で, これを利用してPriority Queueの自分の下に要素がある要素は全体の半分(2分木だから), 前半の要素について後ろから順に…下のほうからPushdownをすれば完全にランダムな配列からも半順序の性質を持たせることができます
この前半のPushdownはソート中のPushDownと違い, ヒープのlog n回のSwap端から端までではなく全体の半分には行わない, 1 / 4には1回しかループしない, 1 / 8には2回しか…その一部分に対して行う操作なので実はO(n)で実行できます
なので全体の実行時間はソート中のPushDownに依存し, n回端から端までのPushDownを行うのでO(n log n)でソートが完了します
実際に集合のうちのBest 5やWorst 10など一部分(端からk個)の情報だけでいいのならこの後半のPushDowsの回数がk回で済むのでO(k log n)になります
中途半端な説明ですがHeapについてはこの辺で, 一度Priority Queueの復習として自分で見てみることをお勧めします