2009/02/09
[解決済] クローゼットのドア問題
この問題が解けたら教えてください, 商品はありません
特にmixiのキング氏とか皆さまのご参加をお待ちしております
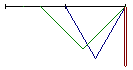
上の図のような2枚の扉からなるクローゼットのドアがあります, ドアの片端は固定されており, もう片方の端はレール上を動きます
このドアの2枚の扉が掃過する領域の形を示してください
(狐がやろうとして投げ出した解法)
ドアの軸を原点において, 扉の動く方向を第1象限にとり, 各扉の長さは1ドアの長さを2とすると, 扉の角度をθとしたとき, 扉のつなぎ目の点は(手が勝手にconsと打ってしまったcosθ, sinθ), レールに固定されている扉の端点は(2cosθ, 0)と表せる
このとき, この2点の間のa:(1-a)内分点の座標は((1+a)cosθ, (1-a)sinθ)となり, 問題の掃過領域とこの点からなる集合は一致する
ここでb=cosθとおいて, x座標を固定し, y座標をxとbの式にして0<b<1での最大値を求めれば, その領域の境界線をxとyの式で表わせそうだなと思い, bで微分して=0としたところで力尽きました
(追記)
ということで, 適当にプログラムを書いて領域の形を作ってみました
自由端側のドアをいっぱい描画しただけです

こんな形になるようです
(さらに追記)
キング氏が, 数学的にこの問題の解を与えてくれました(要mixiアカウント)
また, ymatsux氏にもコメントで分りやすい式を提示していただきました
もっと簡単なものになると思いきや, 結構面倒な解法になるみたいですね
まぁ, インテリアプランナーとかをやっているひとは, これに余裕を持たせた単純な近似式を使ってるんだろうなぁ
参加していただいた皆様ありがとうございました
Comments (6):